RADAR TEGAL – Kunci jawaban matematika kelas 8 halaman 93 sampai 95 semester 2, akan artikel ini bahas selengkapnya.
Jawaban matematika kelas 8 SMP halaman 93 sampai 95, terkait materi Ayo Kita Berlatih 7.3 bagian B esai. Yakni nomor 1-12 dan cara lengkapilah tabel berikut.
Kunci jawaban matematika kelas 8 ini masih berupa pertanyaan yang ada pada buku paket siswa yang masih menggunakan Kurikulum 2013.
Materinya terkait pembahasan tentang lingkaran di Bab 7. Soal-soalnya terdapart dalam buku paket siswa Matematika kelas 8 di Semester 2
Karenanya, siswa yang mengalami kesulitan bisa melihat kunci jawaban soal-soal tentang lingkaran di Bab 7 tersebut di sini.
Tidak hanya kunci jawabannya, siswa SMP kelas 8 juga dapat menemukan cara menggarap hingga pembahasan lengkapnya.
Tetapi ingat, gunakan kunci jawaban ini hanya sebagai referensi untuk bahan pembelajaran. Bukan untuk keperluan lainnya.
Ada 12 pertanyaan yang menjadi pembahasan dalam Buku Paket Siswa Matematika kelas 8 SMP/MTs berbasis Kurikulum 2013 Edisi Revisi 2017 keluaran Kemendikbud.
Pembahasan Jawaban Matematika Kelas 8
Di bawah ini adalah kunci jawaban Metematika kelas 8 halaman 93-95 lengkap dengan cara-cara pembahasannya mengutip alumnus FKIP Universitas Jember, Arum Ariyani SPd.
Ayo Kita Berlatih 7.3 Bagian B esai
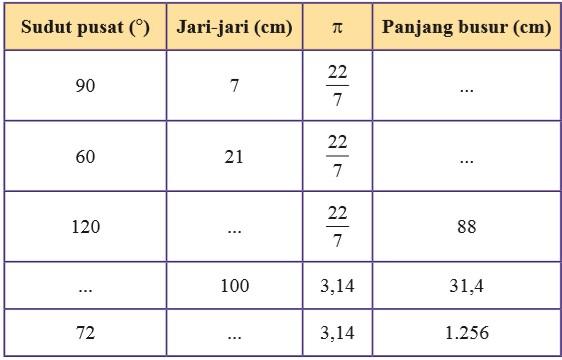
1. Lengkapilah tabel berikut (lihat tabel di buku).
sudut pusat 90° -> panjang busur = 90°/360° x 2 x 22/7 x 7 = 11 cm
sudut pusat 60° -> panjang busur = 60°/360° x 2 x 22/7 x 21 = 22 cm
sudut pusat 120° -> jari-jari = (360°/120° x 88) : (22/7 x 2) = 42 cm
sudut pusat dicari/360° = 31,4 : (2 x 3,14 x 100)
sudut pusat dicari/360° = 1/20
sudut pusat dicari = 1/20 x 360° = 18°
sudut pusat 72° -> jari-jari = (360°/72° x 1.256) : (3,14 x 2) = 1,000 cm
2. Lengkapilah tabel berikut (lihat tabel di buku).
sudut pusat 100° -> luas juring = 100°/360° x 3,14 x 6² = 31,4 cm
sudut pusat 25° -> jari-jari = √(31,4 : (25°/360° x 3,14)) = √144 = 12 cm
sudut pusat dicari/360° = 8.478 : (3,14 x 90²)
sudut pusat dicari/360° = 8.478 : (3,14 x 8100)
sudut pusat dicari/360° = 1/3
sudut pusat dicari = 1/3 x 360° = 120°
3. Tentukan luas juring lingkaran yang diketahui sudut pusatnya 70° dan jari-jarinya 10 cm.
luas juring = 70°/360° x π x r²
luas juring = 70°/360° x 3,14 x 10² = 61,05 cm
4. Tentukan panjang busur lingkaran dengan sudut pusatnya 35o dan jari-jarinya 7 cm.
panjang busur = 35°/360° x 2 x π x r
panjang busur = 35°/360° x 2 x 22/7 x 7 = 4,28 cm
5. Lingkaran A memiliki jari-jari 14 cm. Tentukan sudut pusat dan jari jari suatu juring lingkaran lain agar memiliki luas yang sama dengan lingkaran A.
Luas lingkaran A = π x r² = 22/7 x 14² = 616 cm², misal sudut pusat 90°, maka
L lingkaran A = L juring = 90°/360° x π x r²
616 = 90°/360° x 22/7 x r²
r² = 616 x 360°/90° x 7/22
r = √784 = 28
maka luas juring dengan sudut pusat 90° dan jari-jari 28 memiliki luas yang sama dengan lingkaran A.
6. Buatlah lingkaran A dengan jari-jari tertentu, sedemikian sehingga luasnya sama dengan juring pada lingkaran B dengan sudut pusat dan jari-jari tertentu. Jelaskan?
Misal lingkaran A memiliki jari-jari 28 cm, maka luas A = 22/7 x 28² = 2.464 cm²
misal diambil juring B dengan sudut pusat 60°, maka jari-jarinya agar memiliki luas juring yang sama dengan luas A
L lingkaran A = L juring B = 60°/360° x π x r²
2.464 = 180°/360° x 22/7 x r²
r² = 2.464 x 360°/180° x 7/22
r = √1568 = 28√2 cm
maka lingkaran A dapat dibuat dengan jari-jari 28 cm, lalu lingkaran B memiliki juring dengan sudut 180° dan jari-jari 28√2 cm.
7. Diketahui: (1) lingkaran penuh dengan jari-jari r, (2) setengah lingkaran dengan jari-jari 2r. Tentukan manakah yang kelilingnya lebih besar?
Misal r = 10
Kasus 1:
Keliling = 2πr = 2 x 3,14 x 10 = 62,8 cm
Kasus 2:
Keliling = ½ x 2π(2r) + 2r = ½ x 2 x 3,14 (2×10) + (2 x 10) = 82,8 cm
Maka setengah lingkaran dengan jari-jari 2r memiliki keliling yang lebih besar.
8. Pada gambar di samping (lihat gambar di buku) adalah dua lingkaran yang konsentris di titik pusat E. Jika m∠1 = 42°, tentukan syarat apa yang harus dipenuhi agar panjang busur AB sama dengan dua kali panjang busur CD.
Panjang busur lingkaran kecil (CD) = 42°/360° x 2πr
Panjang busur lingkaran besar (AB) = 42°/360° x 2πR
CD/AB = (42°/360° x 2πr)/(42°/360° x 2πR)
1/2 = (42°/360° x 2πr)/(42°/360° x 2πR)
1/2 = r/R
Maka perbandingan r : R = 1 : 2, sehingga untuk membuat AB = 2CD, maka jari-jari AE = 2DE.
9. Bandingkan keliling lingkaran E dengan persegi panjang ABCD pada gambar di samping (lihat gambar di buku). Tentukan pernyataan yang benar.
Misal r = 10
Keliling persegi panjang ABCD = 2 (p + l) = 2 (2r + r) = 2(3r) = 6r = 60 cm
Keliling lingkaran E = 2πr = 2 x 3,14 x r = 6,28r = 62,8 cm
a. Keliling persegi panjang ABCD lebih dari keliling lingkaran E (salah)
b. Keliling lingkaran E lebih dari persegi panjang ABCD (benar)
c. Keliling lingkaran E sama dengan persegi panjang ABCD (salah)
d. Tidak cukup informasi untuk menentukan perbandingan kelilingnya (salah)
10. Berikut ini diberikan gambar tiga persegi dengan ukuran sama (lihat gambar di buku). Di dalam persegi tersebut dibuat lingkaran sesuai dengan gambar berikut. Daerah di dalam persegi namun di luar lingkaran diberi arsir. Di antara gambar berikut tentukan daerah arsiran terluas.
Luas arsiran gambar kiri:
= (sisi x sisi) – (π x r²)
= (a x a) – (π x (½a)²)
= a² – (22/7 x ¼a²)
= a² – 11/14 a² = 3/14 a²
Luas arsiran gambar tengah:
= (sisi x sisi) – (4π x r²)
= (a x a) – (4π x (¼a)²)
= a² – (4 x 22/7 x 1/16 a²)
= a² – 11/14 a² = 3/14 a²
Luas arsiran gambar kanan:
= (sisi x sisi) – (16π x r²)
= (a x a) – (16π x (⅛a)²)
= a² – (16 x 22/7 x 1/64 a²)
= a² – 11/14 a² = 3/14 a²
Dari hasil perhitungan di atas maka ketiga gambar persegi memiliki luar arsiran yang sama besar.
11. Suatu pabrik biskuit memproduksi dua jenis biskuit berbentuk cakram dengan ketebalan sama, tetapi diameternya beda. Permukaan kue yang kecil dan besar masing-masing berdiameter 7 cm dan 10 cm.
Biskuit tersebut dibungkus dengan dua kemasan berbeda. Kemasan biskuit kecil berisi 10 biskuit dijual dengan harga Rp7.000,00 sedangkan kemasan biskuit besar berisi 7 biskuit dijual dengan harga Rp10.000,00.
Manakah yang lebih menguntungkan, membeli kemasan biskuit yang kecil atau yang besar? Jelaskan alasanmu.
Untuk melihat mana yang lebih untuk maka perlu dihitung volume masing masing biskuit, misal ketebalan biskuit 1 cm.
V biskuit kecil = π x r² x t = 3,14 x 3,5² x 1 = 38,465
V biskuit kecil = π x r² x t = 3,14 x 5² x 1 = 78,5
Isi total kemasan biskuit kecil = 10 x 38,465 = 384,65
Isi total kemasan biskuit besar = 7 x 78,5 = 549,5
Harga per 1 cm³ biskuit kecil = Rp7.000 : 384,65 = 18,198362
Harga per 1 cm³ biskuit besar = Rp10.000 : 549,5 = 18,198362
Baik biskuit kecil dan besar harga per 1 cm³ sama yakni Rp18,198362, maka tidak ada yang lebih untung. Hal ini dipustuskan setelah menghitung harga biskuit per 1 cm³.
12. Suatu ketika anak kelas VIII SMP Semangat 45 mengadakan study tour ke Kebun Raya Pasuruan. Guru menugasi siswa untuk memperkirakan diameter suatu pohon yang cukup besar.
Erik, Dana, Veri, Nia, dan Ria, berinisiatif untuk menghitung diameter pohon tersebut dengan mengukur keliling pohon. Mereka saling mengaitkan ujung jari seperti terlihat pada gambar.
Rata-rata panjang dari ujung jari kiri sampai ujung jari kanan setiap siswa adalah 120 cm. Jika tepat lima anak tersebut saling bersentuhan ujung jarinya untuk mengelilingi pohon tersebut, bisakah kalian menentukan (perkiraan) panjang diameter pohon tersebut.
Keliling pohon = 5 x 120 cm = 600 cm
Keliling = π x d
d = keliling : π
d = 600 : 3,14 = 191,08 cm
Jawaban di atas hanya sebagai alternatif jawaban. Adik-adik boleh mengembangan atau menuliskan jawaban dengan gaya bahasa adik-adik sendiri. Terus semangat dan jangan lupa belajar.
Sebagai catatan, artikel materi ini merupakan pendamping bagi para orang tua untuk pembelajaran anaknya, jawaban bersifat terbuka.
Demikian informasi tentang kunci jawaban Matematika kelas 8 halaman 93-95 Semester 2. Artikel ini tidak mutlak menjamin kebenaran jawaban.***